Méthode de Quine-Mc Cluskey

La méthode de Quine-McCluskey est un algorithme systématique pour minimiser une fonction booléenne quelconque, développé par Willard V. Quine, puis étendu par Edward J. McCluskey^,,.

Principe de la méthode

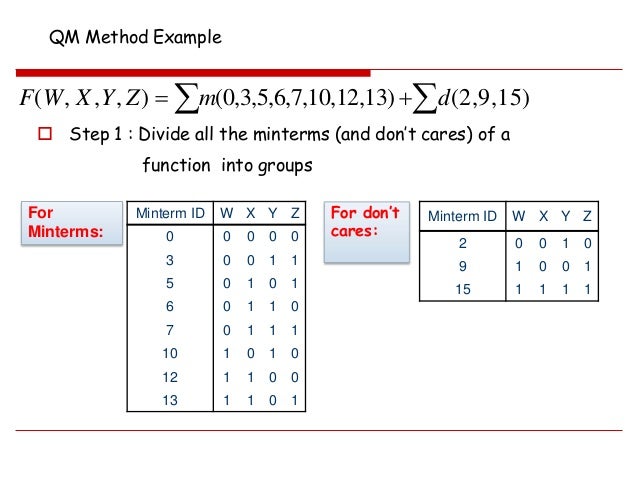
L'algorithme se déroule en deux étapes. Pour faciliter la mise en œuvre de la méthode, la fonction logique doit être exprimée soit sous forme tabulaire (table de vérité, tableau de Karnaugh), soit sous la forme suivante :

${\displaystyle f(A_{0},...,A_{N-1})=R(N_{0},...,N_{k-1}) \Phi (M_{0},...,M_{p-1})}$

où ${\displaystyle (N_{0},...,N_{k-1})}$ sont ${\displaystyle k}$ valeurs (exprimées en binaire ou plus souvent en décimal) correspondant aux ${\displaystyle k}$ cas où ${\displaystyle f(A_{0},...,A_{N-1})}$, avec le nombre ${\displaystyle (A_{N-1}...A_{0})=N_{k}}$, vaut 1 et ${\displaystyle (M_{0},...,M_{p-1})}$ sont ${\displaystyle p}$ valeurs correspondant aux ${\displaystyle p}$ cas où ${\displaystyle f(A_{0},...,A_{N-1})}$, avec le nombre ${\displaystyle (A_{N-1}...A_{0})=M_{p}}$ est indéterminé. Par exemple, l'expression d'une porte NAND sous cette forme serait : ${\displaystyle f_{NAND}(a,b)=R(0,1,2)}$.

La première étape de l'algorithme correspond à la recherche de l'ensemble des termes générateurs. Un terme est générateur s'il ne peut être combiné avec aucun autre terme pour donner un terme plus simple.

Par exemple, dans le cas de la porte NAND, la fonction vaut 1 lorsque ${\displaystyle (ab)}$ vaut ${\displaystyle 00}$, ${\displaystyle 01}$ ou ${\displaystyle 10}$. Le terme ${\displaystyle 00}$ n'est pas un terme générateur car combiné avec ${\displaystyle 01}$, il donne naissance à un terme plus simple ${\displaystyle 0x}$. En revanche, ${\displaystyle 0x}$ ne peut être combiné avec un autre terme, c'est donc un terme générateur. De la même manière ${\displaystyle x0}$ est un autre terme générateur.

Pour trouver les termes générateurs, on utilise les valeurs ${\displaystyle (N_{0},...,N_{k-1})}$ et ${\displaystyle (M_{0},...,M_{p-1})}$ car, comme dans un tableau de Karnaugh, les termes indéterminés peuvent conduire à des simplifications.

La deuxième étape de l'algorithme correspond à l'élimination, parmi les termes générateurs, des termes redondants. Pour cela, on identifie les termes générateurs à partir desquels chaque ${\displaystyle (n_{0},...,n_{k-1})}$ peut-être écrit et on élimine ceux qui sont en trop.

Par exemple, dans le cas de la porte NAND, le terme ${\displaystyle 00}$ et ${\displaystyle 01}$ peuvent être écrit avec le terme générateur ${\displaystyle 0x}$ mais celui-ci n'est pas utilisable pour écrire ${\displaystyle 10}$. L'utilisation du second générateur ${\displaystyle x0}$ est indispensable. Il n'y a pas de terme redondant.

Pour cette étape de simplification, on ne cherche à coder que les valeurs ${\displaystyle (N_{0},...,N_{k-1})}$. Les valeurs indéterminés nous sont ici inutiles.

Illustration sur un exemple

Table de vérité

Considérons la table de vérité suivante

L'exemple n'est pas totalement fortuit. Il s'agit en fait de la table de vérité servant au codage de la barre située en bas à gauche d'un afficheur 7 segments (allumée quand on souhaite afficher 0, 2, 6 ou 8, éteinte quand on a comme code 1, 3, 4, 5, 7 ou 9 et indéterminée pour les codes supérieurs à 9). L'expression de S s'écrit donc

${\displaystyle S=R(0,2,6,8) \Phi (10,11,12,13,14,15)}$

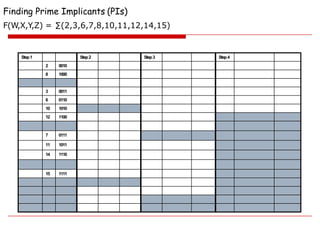
Étape n°1 : Identification des termes générateurs

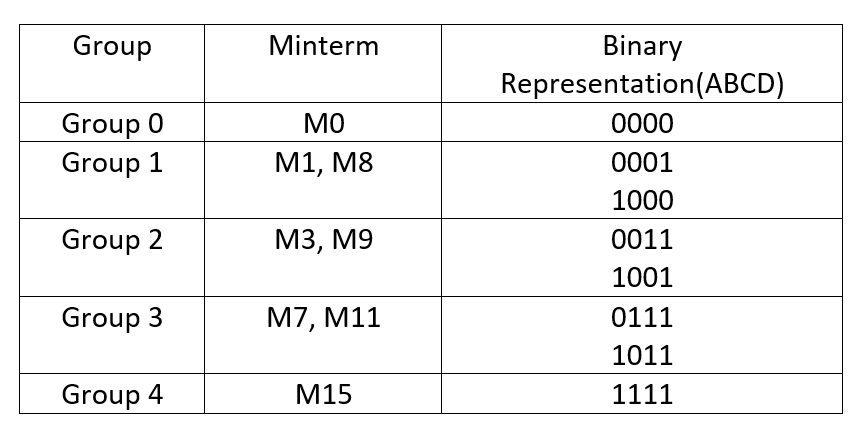
Pour identifier les termes générateurs, on remplit un premier tableau de la manière suivantes : 1°) Dans la première colonne, on écrit tous les termes portant la fonction à 1 ou à une forme indéterminée. Les termes sont triés en fonction du nombre de 1 qu'ils contiennent.

On tente alors de combiner les termes afin d'éliminer ceux qui ne sont pas générateurs. L'intérêt de les avoir triés en fonction du nombre de 1 qu'ils contiennent permet de simplifier cette étape. Dans la colonne 0, on raye tour à tour les termes utilisés dans une recombinaison et on inscrit dans la colonne 1 du tableau les termes issues de ces recombinaisons.

• 0000 peut être recombiné avec 0010 pour former le terme 00x0.
• 0000 peut être recombiné avec 1000 pour former le terme x000.
• 0010 peut être recombiné avec 1010 pour former le terme x010.
• etc ...

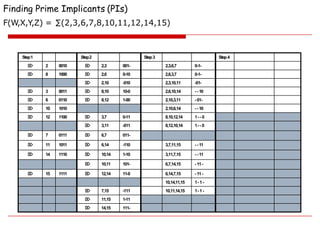
On réitère alors cette opération avec les termes de la Colonne 1 : dans la colonne 1, on raye tour à tour les termes utilisés dans une recombinaison et on inscrit dans la colonne 2 du tableau les termes issues de ces recombinaisons. Ces termes sont composés de 2 x.

• 00x0 peut être recombiné avec 10x0 pour former le terme x0x0.
• x000 peut être recombiné avec x010 pour former le terme x0x0.
• 0x10 peut être recombiné avec 1x10 pour former le terme xx10.
• etc ...
• x110 peut être recombiné avec x010 pour former le terme xx10.

On réitère ce mécanisme jusqu'à ce qu'on ne puisse plus combiner de termes. Dans ce cas, tous les termes de la colonne 2 sont générateurs, mais dans d'autre cas de figure, on pourrait trouver une colonne 3 avec des termes portant 3x.

On a donc identifié 5 termes générateurs : x0x0, xx10, 1xx0, 1x1x et 11xx.

Étape n°2 : Suppression des redondances

Pour identifier les termes redondants, on remplit un second tableau de la manière suivante : - en colonne, on retrouve les termes générateurs - en ligne, on retrouve les termes à exprimer (uniquement ceux de l'expression R puisque les cas indéterminés ne sont pas à coder). - dans les cases, on identifie quel terme générateur est utilisé pour écrire le terme à exprimer.

Le terme x0x0 est à conserver car il est indispensable pour exprimer 0000. Le terme xx10 est à conserver car il est indispensable pour exprimer 0110. x0x0 et xx10 sont nécessaires. De plus, ils sont suffisants : ils réalisent déjà tous les termes de R.

1xx0 ne réalise rien de nouveau ; 1x1x et 11xx n'expriment que des termes de ${\displaystyle \Phi }$, ils sont donc également considérés comme redondants.

Résultat final

Les termes conservés étant ${\displaystyle x0x0(x{\bar {B}}x{\bar {D}})}$ et ${\displaystyle xx10(xxC{\bar {D}})}$, on obtient : ${\displaystyle S={\bar {B}}\cdot {\bar {D}} C\cdot {\bar {D}}}$

Références

• Portail de la logique
• Portail de l'informatique théorique